Colouring the 1-skeleton of $d$-dimensional triangulations
Planken, Tim1
1 Faculty of Mathematics and Computer Science, TU Freiberg, Germany
Innovations in Graph Theory, Volume 2 (2025), pp. 275-299

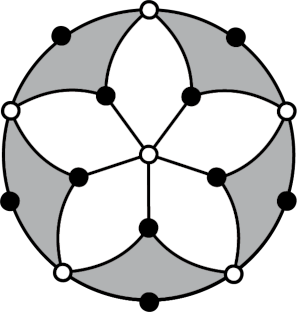
While every plane triangulation is colourable with three or four colours, Heawood showed that a plane triangulation is 3-colourable if and only if every vertex has even degree. In $d \ge 3$ dimensions, however, every $k \ge d+1$ may occur as the chromatic number of some triangulation of $\mathbb{S}^d$. As a first step, Joswig [14] structurally characterised which combinatorial triangulations of $\mathbb{S}^d$ have a $(d+1)$-colourable 1-skeleton. In the 20 years since Joswig’s result, no characterisations have been found for any $k>d+1$.

In this paper, we structurally characterise which combinatorial triangulations of $\mathbb{S}^d$ have a $(d+2)$-colourable 1-skeleton: they are precisely the combinatorial triangulations that have a subdivision such that for every $(d-2)$-cell, the number of incident $(d-1)$-cells is divisible by three.

Received:
Accepted:
Published online:
DOI: 10.5802/igt.13
Classification: 05C15, 05E45, 05C10
Keywords: colouring, triangulation, simplicial complex, Heawood’s theorem, four colour theorem

Planken, Tim 1

1 Faculty of Mathematics and Computer Science, TU Freiberg, Germany
License: CC-BY 4.0
Copyrights: The authors retain unrestricted copyrights and publishing rights 
@article{IGT_2025__2__275_0,
     author = {Planken, Tim},
     title = {Colouring the 1-skeleton of $d$-dimensional triangulations},
     journal = {Innovations in Graph Theory},
     pages = {275--299},
     year = {2025},
     publisher = {Stichting Innovations in Graph Theory},
     volume = {2},
     doi = {10.5802/igt.13},
     language = {en},
     url = {https://igt.centre-mersenne.org/articles/10.5802/igt.13/}
}
TY  - JOUR
AU  - Planken, Tim
TI  - Colouring the 1-skeleton of $d$-dimensional triangulations
JO  - Innovations in Graph Theory
PY  - 2025
SP  - 275
EP  - 299
VL  - 2
PB  - Stichting Innovations in Graph Theory
UR  - https://igt.centre-mersenne.org/articles/10.5802/igt.13/
DO  - 10.5802/igt.13
LA  - en
ID  - IGT_2025__2__275_0
ER  - 
%0 Journal Article
%A Planken, Tim
%T Colouring the 1-skeleton of $d$-dimensional triangulations
%J Innovations in Graph Theory
%D 2025
%P 275-299
%V 2
%I Stichting Innovations in Graph Theory
%U https://igt.centre-mersenne.org/articles/10.5802/igt.13/
%R 10.5802/igt.13
%G en
%F IGT_2025__2__275_0
Planken, Tim. Colouring the 1-skeleton of $d$-dimensional triangulations. Innovations in Graph Theory, Volume 2 (2025), pp. 275-299. doi: 10.5802/igt.13

[1] Appel, Kenneth; Haken, Wolfgang Every Planar Map is Four Colorable, Contemporary Mathematics, American Mathematical Society, 1989 | DOI | Zbl | MR

[2] Basak, Tathagata Combinatorial cell complexes and Poincaré duality, Geom. Dedicata, Volume 147 (2010) no. 1, pp. 357-387 | DOI | Zbl | MR

[3] Carmesin, Johannes Personal communication, 2023

[4] Carmesin, Johannes Embedding simply connected 2-complexes in 3-space (2023) | arXiv | Zbl

[5] Carmesin, Johannes; Mihaylov, Tsvetomir Outerspatial 2-complexes: Extending the class of outerplanar graphs to three dimensions (2021) | arXiv

[6] Carmesin, Johannes; Nevinson, Emily; Saunders, Bethany A characterisation of 3-colourable 3-dimensional triangulations (2022) | arXiv | Zbl

[7] Diestel, Reinhard; Jacobs, Raphael W; Knappe, Paul; Kurkofka, Jan Canonical graph decompositions via coverings (2022) | arXiv | Zbl

[8] Garey, Michael R.; Johnson, David S.; Stockmeyer, Larry Some simplified NP-complete graph problems, Theor. Comput. Sci., Volume 1 (1976) no. 3, pp. 237-267 | DOI | Zbl | MR

[9] Georgakopoulos, Agelos; Kim, Jaehoon 2-complexes with unique embeddings in 3-space, Bull. Lond. Math. Soc., Volume 55 (2022) no. 1, pp. 156-174 | Zbl | DOI | MR

[10] Golovina, Lidiia Ivanovna; Yaglom, Isaak Moiseevitch Induction in geometry, D. C. Heath & Co., 1963

[11] Hatcher, Allen Algebraic topology, Cambridge University Press, 2002, xii+544 pages | MR | Zbl

[12] Heawood, Percy J. On the four-colour map theorem, Quart. J., Volume 29 (1898), pp. 270-285 | Zbl

[13] Hopcroft, John; Tarjan, Robert Efficient Planarity Testing, J. ACM, Volume 21 (1974) no. 4, pp. 549-568 | DOI | Zbl

[14] Joswig, Michael Projectivities in simplicial complexes and colorings of simple polytopes, Math. Z., Volume 240 (2002) no. 2, pp. 243-259 | DOI | Zbl | MR

[15] Król, Mieczysław On a sufficient and necessary condition of 3-colorableness for the planar graphs. I, Prace Nauk. Inst. Mat. Fiz. Teoret. Politechn. Wroc law Ser. Studia i Materia ly, Volume 1972 (1972) no. 6, pp. 37-40 | Zbl | MR

[16] Kühnel, Wolfgang Triangulations of manifolds with few vertices, World Scientific, 1990, pp. 59-114 | DOI | Zbl

[17] Kurkofka, Jan; Nevinson, Emily On the edge-chromatic number of 2-complexes, Discrete Math., Volume 348 (2025) no. 2, Paper no. 114309 | DOI | Zbl | MR

[18] Lovász, László Combinatorial problems and exercises, American Mathematical Society, 2007 | MR | Zbl

[19] Mendelsohn, Eric; Rosa, Alexander One-factorizations of the complete graph—a survey, J. Graph Theory, Volume 9 (1985) no. 1, pp. 43-65 | DOI | MR | Zbl

[20] Munkres, James R. Elements of Algebraic Topology, CRC Press, 2018 | DOI | MR

[21] Robertson, Neil; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin Efficiently four-coloring planar graphs, Proceedings of the twenty-eighth annual ACM symposium on Theory of computing - STOC '96, ACM Press (1996), pp. 571-575 | DOI | Zbl

[22] Tsai, Mu-Tsun; West, Douglas B. A new proof of 3-colorability of Eulerian triangulations, Ars Math. Contemp., Volume 4 (2011) no. 1, pp. 73-77 | MR | DOI | Zbl

[23] Ziegler, Günter M. Lectures on Polytopes, Graduate Texts in Mathematics, Springer, 1995 | DOI | Zbl | MR

Cited by Sources: